数学概念

​ 越学习计算机越感觉要有一定数学知识才能编写可用的算法，因此，单独记录一下常用的数学基础概念、公式、推理等。

素数（质数）

概念

在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

素数生成算法

1、埃拉托斯特尼筛法

这是一种用于生成素数的筛法。

基本步骤：从最小的素数2开始，将该素数的所有倍数标记成合数，而下一个尚未被标记的最小自然数3即是下一个素数。如此重复这一过程，将各个素数的倍数标记为合数并找出下一个素数，最终便可找出一定范围内所有素数。

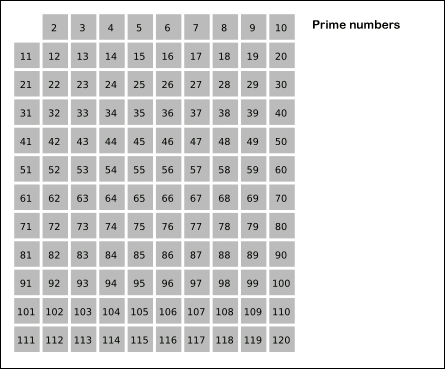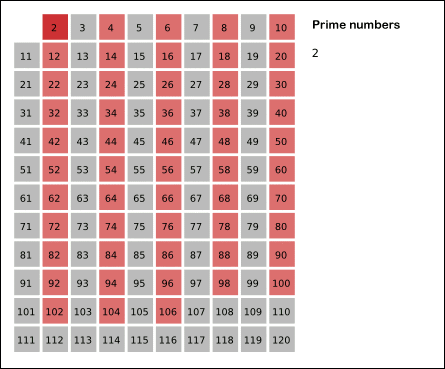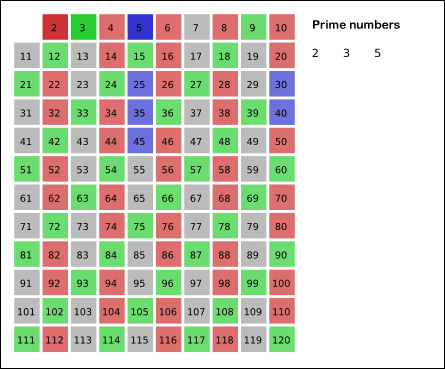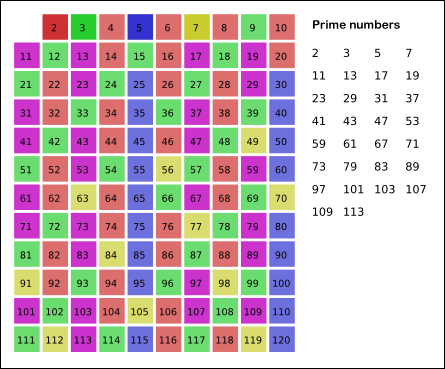
如下图所示：使用埃拉托斯特尼筛法找出120以内的所有素数。由于，当11成为最小的未标记整数时，尚未标记的所有数皆可确认为素数。

请注意到在标记时直接从每个素数的平方开始。

在使用这种筛法，寻找素数时，并不需要对范围内所有整数查找，也不需要对每个素数都标记所有倍数。

通常有一定规律可以简化筛选过程：

1. 寻找以内的素数时，若找到了一个大于的素数，则剩余的所有尚未标记的数也都是素数。
2. 标记某一素数的倍数时，不需要每次皆从开始，而可直接从开始标记。

• 利用上述规律改进的埃拉托斯特尼筛法找出25以内的素数具体过程如下：

伪代码表示：

1
2
3
4
5
6
7
8
9
10
11

输入：整数n > 1
 
设A为布尔值矩阵，下标是2至n的整数，
初始时全部设成true。
 
 for i = 2, 3, 4, ..., 不超过sqrt(n)：
  if A[i]为true：
    for j = i^2, i^2+i, i^2+2i, i^2+3i, ..., 不超过n：
      A[j] := false
 
输出：使A[i]为true的所有i。

算法实现代码：

1
2
3
4
5
6
7
8

def eratosthenes(n):
    is_prime = [True] * (n + 1)
    for i in range(2, int(n ** 0.5) + 1):
        if is_prime[i]:
            for j in range(i * i, n + 1, i):
                is_prime[j] = False
    return [x for x in range(2, n + 1) if is_prime[x]]
print(eratosthenes(120)) #筛选出120以内的素数

埃拉托斯特尼筛法的时间复杂度 为

互质数

概念

两个或多个整数的公因数只有1的非零自然数

常用判断方法

1、概念判断法

公约数只有1的两个数叫做互质数。根据互质数的概念可以对一组数是否互质进行判断。如：9和11的公约数只有1，则它们是互质数。 [3]

2、规律判断法

根据互质数的定义，可总结出一些规律，利用这些规律能迅速判断一组数是否互质。 [4]

（1）两个不相同的质数一定是互质数。如：7和11、17和31是互质数。

（2）两个连续的自然数一定是互质数。如：4和5、13和14是互质数。

（3）相邻的两个奇数一定是互质数。如：5和7、75和77是互质数。

（4）1和其他所有的自然数一定是互质数。如：1和4、1和13是互质数。

（5）两个数中的较大一个是质数，这两个数一定是互质数。如：3和19、16和97是互质数。

（6）两个数中的较小一个是质数，而较大数是合数且不是较小数的倍数，这两个数一定是互质数。如：2和15、7和54是互质数。

（7）较大数比较小数的2倍多1或少1，这两个数一定是互质数。如：13和27、13和25是互质数。

3、分解判断法

如果两个数都是合数，可先将两个数分别分解质因数，再看两个数是否含有相同的质因数。如果没有，这两个数是互质数。 [5]如：130和231，先将它们分解质因数：130=2×5×13，231=3×7×11。分解后，发现它们没有相同的质因数，则130和231是互质数。

4、求差判断法

如果两个数相差不大，可先求出它们的差，再看差与其中较小数是否互质。如果互质，则原来两个数一定是互质数。如：194和201，先求出它们的差，201－194=7，因7和194互质，则194和201是互质数。

5、求商判断法

用大数除以小数，如果除得的余数与其中较小数互质，则原来两个数是互质数。如：317和52，317÷52=6……5，因余数5与52互质，则317和52是互质数。

欧拉函数

概念

对于正整数n，欧拉函数φ(n)是小于等于n的正整数中，与n为互质数的个数。例如φ(8) = 4，因为1,3,5,7均和8互质。

标准分解式

将质因数分解的结果，按照质因数大小，由小到大排列，并将相同质因数的连乘积，以指数形式表示。

例如：

2020的标准分解式为 $2020=2^25101$

计算方法

1、先化为标准分解式：

​

2、按照如下规则计算

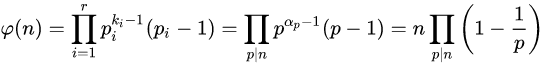
例如：

注意：

1、，则，因为11与任何数（包括自身）都构成互质关系。

2、是质数，如果是质数，则，因为质数与小于它的每一个数，都构成互质关系。

3、如果是质数的某一个次方，即(p为质数，k为大于等于1的整数)，则

比如

4、如果n可以分解成两个互质的整数之积，，则
即积的欧拉函数等于各个因子的欧拉函数之积。比如，

5、欧拉函数通用计算公式：

公因数

概念

一个能同时整除若干整数的整数。

比如 $-27 = -39，18=29$，那么9就是-27和18的公因数，同时也是最大公因数。

求最大公因数方法

1、辗转相除法

辗转相除法又称为欧几里得算法，用于计算两个正整数a,b的最大公约数和最小公倍数。

在python的math库中可以直接调用：

1
2
3

math.gcd(a,b)
#返回给定的整数参数a,b的最大公约数
#在python3.5中该方法被添加，在python3.9中更新：添加了对任意数量的参数的支持，之前的版本只支持两个参数

算法实现过程：

设两数为a,b，其中a 做被除数，b做除数，c为余数
1、大数放a中、小数放b中；
2、求a/b的余数；
3、若c=0则b为最大公约数；
4、如果c!=0则把b的值给a、c的值给a；

1 2 3 4 5

while a % b != 0: c = a % b a = b b = c printf("最大公约数为%d",b);

• 注：这算法的时间复杂度通常被认为O(log(min(a, b)))，

2、更相损减法

基本思想：通过反复地用两个数中较大的数减去较小的数，直到两个数相等为止。

用一个简单的递归函数来实现：

1
2
3
4
5
6
7
8
9
10
11

def gcd(a, b):
    if a == b:
        return a
    elif a > b:
        return gcd(a - b, b)
    else:
        return gcd(a, b - a)

# 示例
result = gcd(12, 18)
print(result)  # 输出为6

• 注：这算法的时间复杂度为O(max(a, b))，它在特定情况下可能会比辗转相除法更快，尤其是当两个数非常接近时。

3、穷举法

基本思想：通过逐个尝试所有可能的因数，从最大的可能因数开始逐渐减小，直到找到两个数的公约数为止。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def gcd(a, b):
    # 确保a大于等于b
    if a < b:
        a, b = b, a
    
    # 从较小的数开始逐个尝试可能的因数
    for i in range(b, 0, -1):
        if a % i == 0 and b % i == 0:
            return i
    
    # 如果没有找到公约数，默认返回1
    return 1

# 示例
result = gcd(12, 18)
print(result)  # 输出为6

• 注：这算法的时间复杂度是 O(min(a, b))，因为它必须尝试所有可能的因数，但它在实际中可能不太适用于大型整数，因为它的效率较低。

4、Stein算法

Stein算法也称为二进制 GCD 算法，是用于计算两个非负整数的最大公约数的一种高效算法。

基本思想：将两个整数 a 和 b 分解成偶数和奇数的形式，然后利用数学性质简化计算。

具体步骤如下：

1. 如果 a 和 b 中有一个是 0，则返回另一个非零整数作为最大公约数。
2. 如果 a 和 b 都是偶数，则最大公约数等于 2 乘以 Stein(a/2, b/2)。
3. 如果 a 是偶数，b 是奇数，则最大公约数等于 Stein(a/2, b)。
4. 如果 a 是奇数，b 是偶数，则最大公约数等于 Stein(a, b/2)。
5. 如果 a 和 b 都是奇数，则最大公约数等于 Stein(|a-b|/2, min(a, b))。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

def stein_gcd(a, b):
    if a == 0:
        return b
    if b == 0:
        return a

    # 计算 a 和 b 的最低位 1 的数量
    shift = 0
    while ((a | b) & 1) == 0:
        a >>= 1
        b >>= 1
        shift += 1

    # 将 a 和 b 变为奇数
    while (a & 1) == 0:
        a >>= 1

    # Stein 算法主体
    while b != 0:
        while (b & 1) == 0:
            b >>= 1

        if a > b:
            a, b = b, a
        b -= a

    # 返回结果
    return a << shift

# 示例
result = stein_gcd(12, 18)
print(result)  # 输出为6

• 注：这个算法的时间复杂度是 O(log(max(a, b)))